Vibration Theory

The Harmonic Oscillator

The Harmonic Oscillator constitutes one of the most fundamental models in vibration theory. Its equations of motion in one dimension are:

where is the displacement of mass from its orginal position, and is a constant. Initial conditions might look something like:

The above equation of motion represents a spring-mass system, i.e., a mass connected to a wall via a spring. The restoring force produced by the spring grows proportionally to and to the displacement of the mass from its origin. Unless , the mass will “vibrate”, i.e. change its position relative to its equilibrium position in a periodic manner.

The equations of motion can be solved either using sines and cosines or a complex exponential Ansatz which we will discuss later. Using trigonometric functions for our proposed solution we have

At we assume initial conditions and , which means . With that the final solution becomes:

which shows that the mass moves periodically about the center.

Eigenfrequencies

A 1D Harmonic Oscillator such as we discussed above has precisely one period of oscillation, and, thus, one eigenfrequency . This frequency shows up in the and terms of our soltuion. Can we connect this frequency to physical parameters in our equation of motion?

If we differentiate our solution twice with respect to time we find

On the other hand, from our equation of motion we know that

Comparing coefficients of on the right hand side of both equations gives:

Dampened Harmonic Oscillator

We can use Newtonian Mechanics to study the impact of adding a damping force to a harmonic oscillator:

For linear restitution and damping proportional to velocity our equation of motion (EoM) reads

Using a complex exponential Ansatz, i.e., and . Inserting this into the EoM we find

which lets us calculate the eigenfrequencies

Inserting this again into our Ansatz we find the general solution

Looking at the terms in the exponents we can define a damping timescale:

and rewrite the solution as:

Depending on the system this solution permits three kinds of behavior

• Underdamped (oscillatory):
• Critically damped (fastest damping):
• Overdamped (slow damping):

In order to convince ourselves that there is still some oscillatory behavior we can define and rewrite the above solution in trigonometric form:

Dampened Driven Harmonic Oscillator

Even more interesting behavior can arise when a harmonic oscillator is driven through an external, periodic force

Assume

Then the equation of motion reads

This is an inhomogeneous differential equation of second order. The solution has to be found through superposition of the homogeneous and a particular solution:

It is useful to rewrite the forcing term as a complex exponential:

We are allowed to do this because

and, thus,

It is again convenient to choose a complex Ansatz since we already know this works for the homogeneous case:

We will furthermore assume that the particular solution can also be expressed in the form:

Plugging the particular solution into the equation of motion results in

so that

Calculating the complex amplitude for the particular solution yields

The particular solution, thus, reads

The total solution then reads

Resonance

Let us investigate the above soltion in more detail. Assuming , we can rewrite the solution as

Rewriting the above equation yields

Defining the scaled amplitude and phase difference

and we can equate real and imaginary parts separately, i.e.,

Squaring both equations

and adding them again gives the magnitude:

Expressing from the previous equation gives

Rewriting the previous equation for the scaled amplitude in a slightly different form yields

and with

where is the so-called “damping ratio”, we can find the amplitude in terms of damping ratio:

Finally, the phase difference between forcing and the response of the harmonic oscillator reads

These equations contain a well-known condition for resonance. If the driving frequency and the natural frequency coincide and damping is insufficient, the amplitude of the driven oscillator increases dramatically.

Coupled Harmonic Oscillators

Coupled harmonic oscillators are used as a model in several different fields to better understand energy exchange between vibrating modes in systems such as airfoils, or buildings subject to external forcing. Taking the example from the lecture, we have two spring mass systems, each coupled to its nearest wall with a spring with a coefficient . The displacement of said masses from their origins is given by and , respectively. Both masses are also coupled with a center spring with a potentially different coefficient .

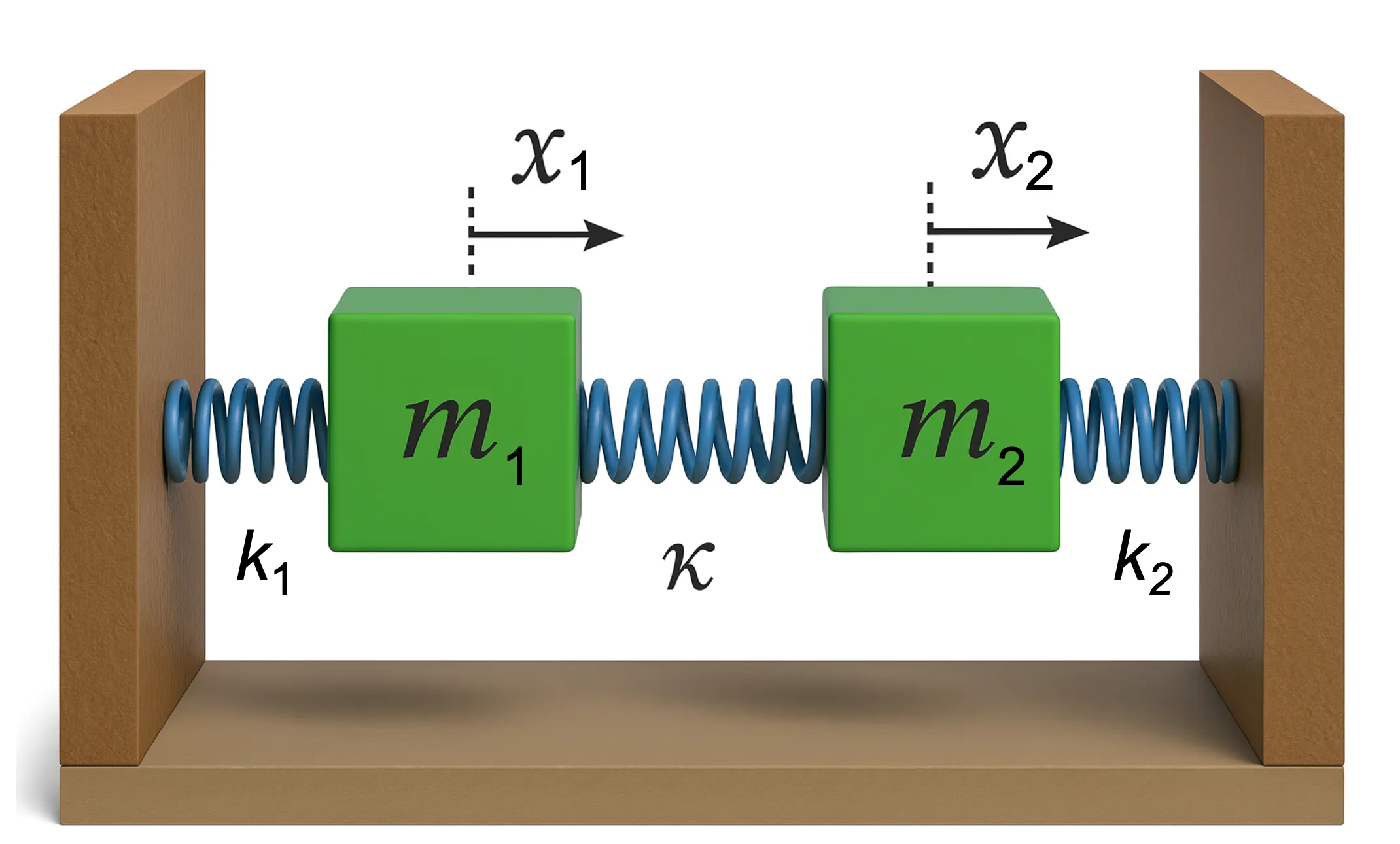
The corresponding equations of motion read

Since the coupling is linear in the states, we can rewrite that system in matrix form

where

and

This step will enable us to elegantly decouple the system by transforming into the Eigensystem of the differential equations via the (mass weighted) coupling matrix . The aim is to transform the system into the following form

where each component is decoupled from each other, so that becomes diagonal. To this end we determine the Eigenvalues () and Eigenvectors () of

and

Using the Eigenvectors we can define a basis change matrix that will allow us to find the new from . This can be achieved by ensuring that has the Eigenvectors of as columns:

Then

and

Similarly, we can find as

which eventually reads

The new, decoupled Eigensystem of harmonic oscillators has the following equations of motion

Those can now be solved conveniently via our standard Ansatz

Inserting the above into the differential equations yields

With corresponding normal/Eigenfrequencies

The Eigenmode solutions then read

In order to translate the Eigenmode solutions into our original coordinates, we need the inverse of our basis transformation matrix :

Example:

Let us assume the two coupled harmonic oscillators are subject to the following initial conditions

Since we already did all the work by transforming the equations of motion in to the decoupled system and solving the latter, we know solutions for explicitly:

Inserting the initial conditions we find

This is a system of two equations with two unknown amplitudes and . The solution for the amplitudes is , which, together with the other initial conditions, gives

Tuned Mass Dampers

A tuned mass damper (TMD) is a device used to reduce the amplitude of mechanical vibrations. It consists of a mass, a damper, and a spring, which is tuned to a specific frequency to counteract resonant vibrations. By adding an auxiliary mass to the structure, which is tuned to a specific frequency, and connected to the main structure through a spring and a damper, the system transfers energy from the vibrating structure to the damper, reducing resonance amplitudes. Tuned mass dampers are widely used in aerospace applications to mitigate unwanted vibrations in structural systems.

Consider a single-degree-of-freedom system with mass , damping , and stiffness . The equation of motion for this system under a harmonic force, for instance, is:

Now, we add a tuned mass damper with mass , damping , and stiffness . The TMD is attached to the primary mass and introduces an additional degree of freedom.

Let be the displacement of the TMD mass. Then, the coupled equations of motion for the combined system are:

The damping force provided by the TMD is proportional to the relative velocity between the two masses, given by:

Tuning the TMD

The goal of tuning is to select the TMD parameters , , and to minimize the vibration amplitude at the resonance frequency of the primary system, , which occurs at:

To tune the TMD we want the natural frequency of the TMD should match the resonance frequency of the primary system:

This ensures that the TMD is tuned to the frequency where the primary system has its largest response. The damping ratio of the TMD, , is chosen to provide optimal damping. A typical choice for optimal damping is to .

Example

Consider a system where the primary mass is , stiffness , and damping . The target resonance frequency is:

For the TMD, we select . To tune the natural frequency of the TMD to , we choose the stiffness of the TMD as:

Now, select the damping ratio to find the damping coefficient of the TMD:

Bode Plots

The TMD is tuned to match the resonant frequency of the primary system. Bode diagrams can be used to visually confirm the reduction in the resonant peak. The figure below shows the tuned parameter configuration from the example below. The blue curve is the frequency response without TMD, the orange one with TMD.

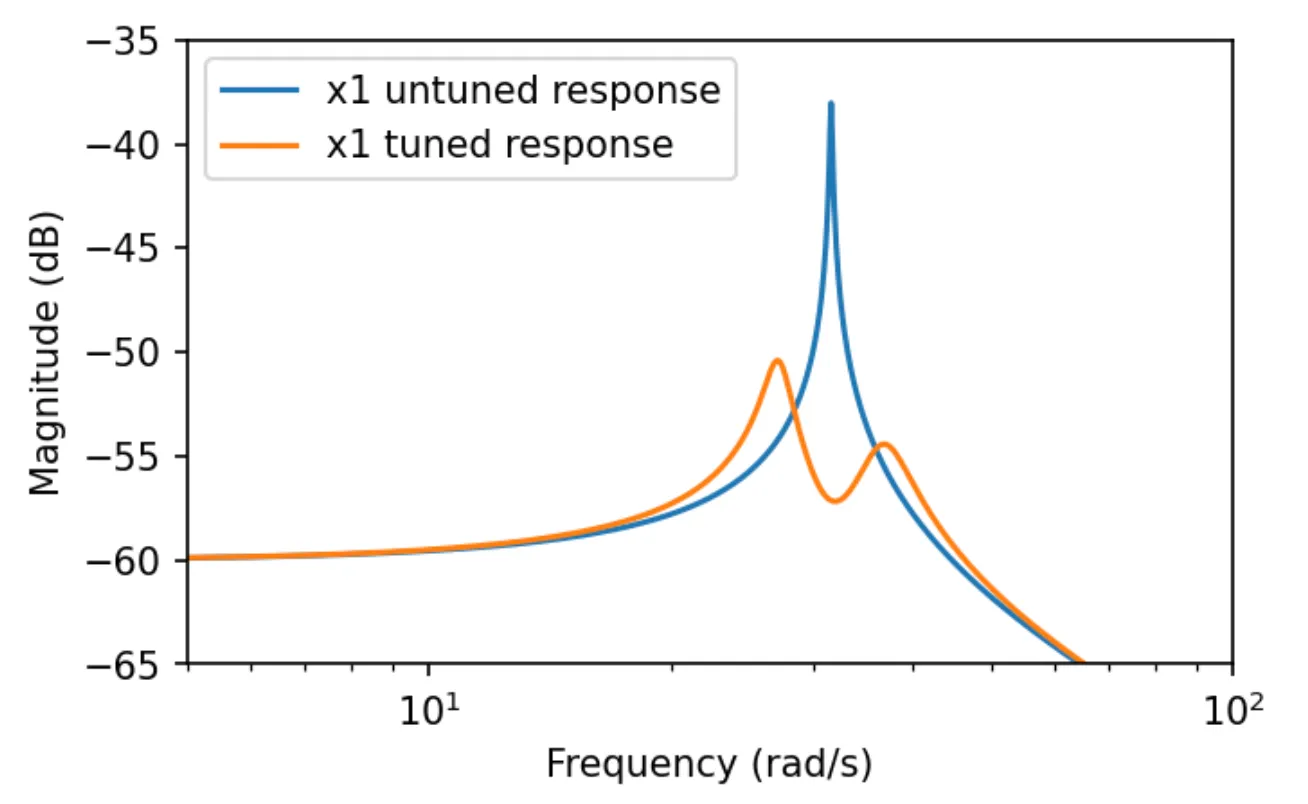
The figure shows that even TMDs that only weigh a fraction of the driving mass can reduce the peak amplitude by a factor of 100 (roughly -20dB power) in the vicinity of the resonance frequency!

Transfer Functions

Using the Transfer Function of a system featuring tuned mass damper is another possible way to tune TMDs. Consider again the single-degree-of-freedom system with mass , damping , and stiffness . The equation of motion is

Taking the Laplace transform yields

The transfer function of this undamped system is then defined as the function relating the displacement to the input force

where . Now, we add a tuned mass damper with mass , damping , and stiffness . The combined system reads

Taking the Laplace transform of the coupled equations (assuming zero initial conditions) and solving for the transfer function relating the displacement to the input force , we get the combined system’s transfer function: