Dynamical Systems Theory

Dynamical systems theory is a mathematical framework used to describe the evolution of systems over time. A dynamical system is characterized by a set of differential equations that describe how the state of a system evolves based on its current state and external inputs. Mathematically, a dynamical system is expressed as a set of first-order ordinary differential equations (ODEs):

where is the state vector representing the system’s state at time , and is a vector-valued, often nonlinear function that determines how the state evolves based on the current state and time. The state generally includes position and velocity, but it can also encompass orientation, and angular velocity, or generalized coordinates and momenta, etc.

For specific initial conditions solutions to the above equations can most often be found either by using analytical or numerical methods for ODEs. In contrast, dynamical systems theory aims at understanding how the entire system behaves both qualitatively and quanitatively, which includes - but is not limited to - potentially stable or unstable behavior, equilibria in state space, and/or strong dependence of the system behavoir on parameters (e.g. bifurcations).

Heads up!

Dynamical systems theory is equally capable of dealing with ordinary differential equations beyond first order. Formally an -th order ordinary differential equation

can be rewrtitten as a system of first-order ODEs

through introducing a set of new variables

Equilibrium Points

Understanding equilibrium points is a cornerstone of dynamical systems theory, offering a window into both local and global properties of complex systems. An equilibrium point (or fixed point) is a state of the system where the evolution ceases, meaning the system remains at rest if it starts at that point. For a system described by

an equilibrium point satisfies

Equilibrium points are central to understanding the long-term behavior of dynamical systems because they often organize the motion of nearby trajectories. By analyzing their stability, one can predict whether small deviations from equilibrium will decay over time, grow uncontrollably, or persist in a neutral fashion.

Heads up!

Studying equilibrium points provides deep insight into the qualitative behavior of a system. They identify the location of steady states and often shape the global organization of trajectories in nonlinear systems, with stable and unstable manifolds acting as pathways that govern the flow of the system. As such studying equilibria in dynamical systems can guide the design of control strategies aimed at stabilizing desired states.

Linearization

Near an equilibrium point, it is common to linearize the system by expanding around :

where represents the state relative to the equilibrium point , and is the Jacobian matrix evaluated at the equilibrium:

The power of linarization becomes evident when we recall that a (full rank) system of linear ODEs permits a general solution of the form

where are eigenvectors of , are the corresponding eigenvalues and are constants. Since the solution is a composition of exponentials of eigenvalues and directions given by eigenvectors, it is the eigenvalues of that determine the nature of the equilibrium. If all eigenvalues have negative real parts, the equilibrium is stable and nearby trajectories are attracted to it. If any eigenvalue has a positive real part, the equilibrium is unstable, causing nearby trajectories to diverge. Equilibria with eigenvalues that have zero real parts require further analysis.

Stable and Unstable Manifolds

A common scenario is that the matrix of the linearized system has some positive and some negative eigenvalues. Consider the following dynamical system

This system has an equilibrium at . The linearized system evaluated at the equilibrium reads

with

has eigenvalues and as well as and . Solutions of the linearized equations are a composit of subspaces, for example

In this context, 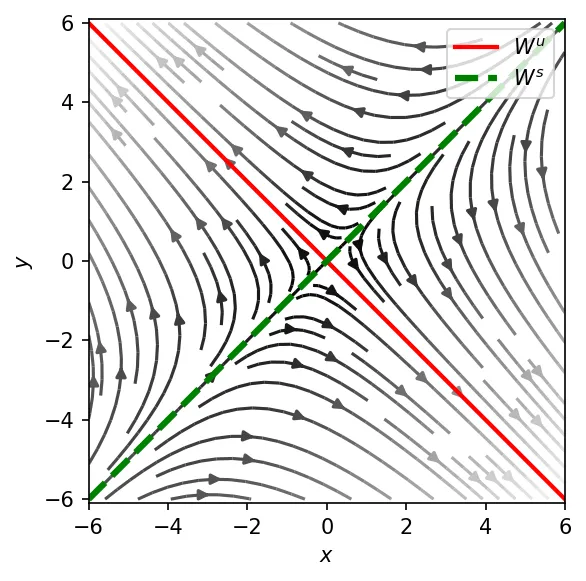would correspond to the local representation of the unstable manifold and to the stable manifold of a hyperbolic equilibrium point. Stable and unstable manifolds for the example dynamical system.

Formally, if is a solution to the dynamical system with initial condition we can define a

Stable manifold as (tangent to) a subspace of a dynamical system where trajectories approach the equilibrium as .

Unstable manifold as (tangent to) a subspace of a dynamical system departing from an equilibrium as .

Center manifold as (tangent to) a (possibly non-unique) subspace of a dynamical system that is spanned by Eigenvalues with zero real part, i.e., .

Stable and unstable manifolds do not have to be one-dimensional. The dimensions of the linear subspaces, and, thus, the manifolds themselves are determined by the eigenvalues of . The dimensions of the stable and unstable manifolds add up with any center manifold to the full dimension of the system.

Let be the number of eigenvalues with negative real part, be the number of eigenvalues with positive real part, and be the number of eigenvalues with zero real part (center directions) that define the center manifold.

Then:

with , where is the dimension of the full system.

Intuitively, the stable manifold spans the directions along which perturbations decay to over time, the unstable manifold spans the directions along which perturbations grow away from , and the center manifold (if any) spans the directions along which dynamics are neither decaying nor growing exponentially.

Bifurcations

A far reaching result in dynamical systems theory is that the behavior of the system can also depend on parameters, for instance, additive or multiplicative constants. A so-called bifurcation occurs when a small smooth change in a system parameter causes a qualitative change in the system’s long-term behavior. Bifurcations indicate where the number or stability of equilibrium points (or periodic orbits) changes, fundamentally altering the system’s dynamics.

Consider a dynamical system depending on a parameter :

where is the state variable and is a system parameter. A bifurcation point occurs when the stability or number of equilibria changes.

Heads up!

Bifurcation analysis is a central tool in understanding how seemingly innocuous parameters cause systems to transition between different behaviors, such as from steady states to oscillations which can be critical in the design of flight and control systems.

One-Parameter Bifurcations

Common examples of bifurcations in one-parameter systems include:

Saddle-node bifurcations: Two equilibria (one stable, one unstable) “collide and annihilate” each other as crosses a critical value. Take for example

For , there are no real equilibria, since implies that . For , a single equilibrium exists at . For , two equilibria appear at , one stable and one unstable. The figure below shows this behavior for

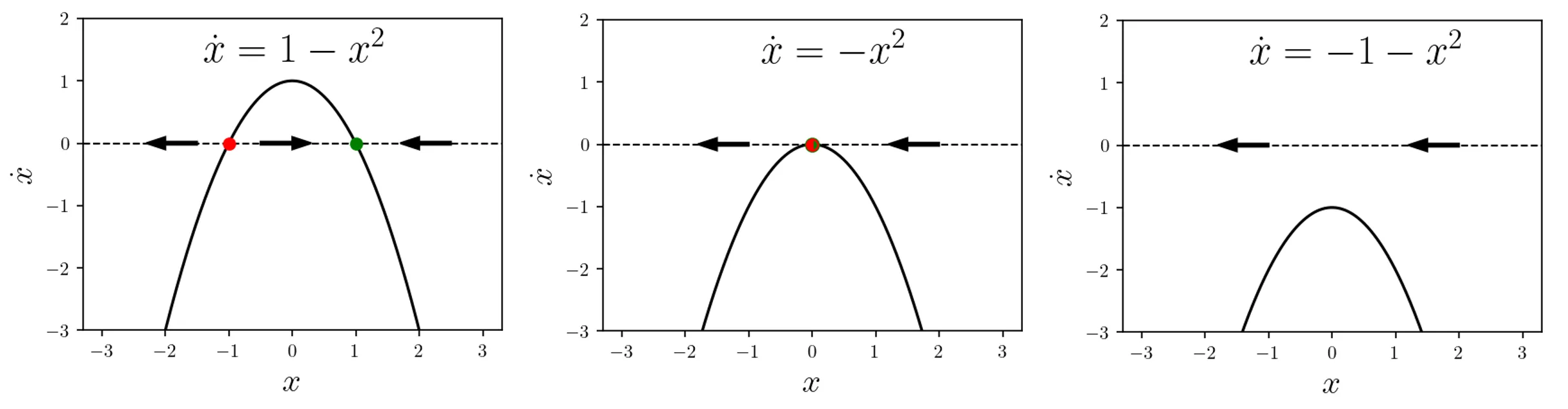
Saddle Node Bifurcation

Pitchfork bifurcations: A symmetric equilibrium loses stability and two new equilibria emerge:

For , is stable. For , becomes unstable and two stable equilibria appear at .
Hopf bifurcations: An equilibrium point loses stability and a small-amplitude limit cycle emerges.

Two-Parameter Bifurcations

When a system depends on two parameters, and , i.e.,

more complex bifurcation structures can occur. Curves in the parameter plane can separate regions with qualitatively different dynamics, and points where multiple bifurcation curves meet are called codimension-2 bifurcations. These can lead to richer phenomena such as Bogdanov–Takens or cusp bifurcations.